Класс Complex

Комплексные числа широко используются не только в математике. Они часто применяются в графических преобразованиях, в построении фракталов, не говоря уже о физике и технических дисциплинах. Но класс, описывающий комплексные числа, почему-то не включен в стандартную библиотеку Java. Восполним этот пробел.

Листинг 2.4 длинный, но просмотрите его внимательно, при обучении языку программирования очень полезно чтение программ на этом языке. Более того, только программы и стоит читать, пояснения автора лишь мешают вникнуть в смысл действий (шутка).

Листинг 2.4. Класс Complex

class Complex {

   private static final double EPS = le-12; // Точность вычислений 

   private double re, im;                   // Действительная и мнимая часть

                                            // Четыре конструктора 

   Complex(double re, double im) { 

      this, re = re; this.im = im;

   }

   Complex(double re){this(re, 0.0); }

   Complex(){this(0.0, 0.0); }

   Complex(Complex z){this(z.re, z.im) ; }

      // Методы доступа 

   public double getRe(){return re;} 

   public double getlmf){return im;} 

   public Complex getZ(){return new Complex(re, im);} 

   public void setRe(double re){this.re = re;} 

   public void setlm(double im){this.im = im;} 

   public void setZ(Complex z){re = z.re; im = z.im;}

      // Модуль и аргумент комплексного числа

   public double mod(){return Math.sqrt(re * re + im * im);} 

   public double arg()(return Math.atan2(re, im);}

      // Проверка: действительное число? 

   public boolean isReal(){return Math.abs(im) < EPS;}

   public void pr(){    // Вывод на экран

      System.out.println(re + (im < 0.0 ? "" : '"+") + im + "i");

   }

      // Переопределение методов класса Object

   public boolean equals(Complex z){ 

      return Math.abs(re -'z.re) < EPS && 

             Math.abs(im - z.im) < EPS;

   }

   public String toString(){

      return "Complex: " + re + " " + im;

   }

      // Методы, реализующие операции +=, -=, *=, /= 

   public void add(Complex z){re += z.re; im += z.im;} 

   public void sub(Complex z){re -= z.re; im —= z.im;} 

   public void mul(Complex z){

      double t = re * z.re — im * z. im; 

            im = re * z.im + im * z.re; 

            re = t;

   }

   public void div(Complex z){

      double m = z.mod();

      double t = re * z.re — im * z.im;

      im = (im * z.re — re * z.im) / m;

      re = t / m; 

   }

      // Методы, реализующие операции +, -, *, / 

   public Complex plus(Complex z){

      return new Complex(re + z.re, im + z im);

   } 

   public Complex minus(Complex z){

      return new Complex(re - z.re, im - z.im); 

   }

   public Complex asterisk(Complex z){ 

      return new Complex(

         re * z.re - im * z.im, re * z.im + im * z re);

   }

public Complex slash(Complex z){ 

   double m = z.mod(); 

   return new Complex(

      (re * z.re - im * z.im) / m, (im * z.re - re * z.im) / m);

   }

}

   // Проверим работу класса Complex 

public class ComplexTest{

   public static void main(Stringf] args){ 

      Complex zl = new Complex(),

              z2 = new Complex(1.5), 

              z3 = new Complex(3.6, -2.2), 

              z4 = new Complex(z3);

      System.out.printlnf);       // Оставляем пустую строку 

      System.out.print("zl = "); zl.pr(); 

      System.out.print("z2 = "); z2.pr(); 

      System.out.print("z3 = "); z3.pr(); 

      System.out.print ("z4 = "}; z4.pr(); 

      System.out.println(z4);     // Работает метод toString()

      z2.add(z3);

      System.out.print("z2 + z3 = "}; z2.pr();

      z2.div(z3);

      System.out.print("z2 / z3 = "); z2.pr(); 

      z2 = z2.plus(z2);

      System.out.print("z2 + z2 = "); z2.pr(); 

      z3 = z2.slash(zl);

      System.out.print("z2 / zl = "); z3.pr(); 

   } 

}

На рис. 2.3 показан вывод этой программы.

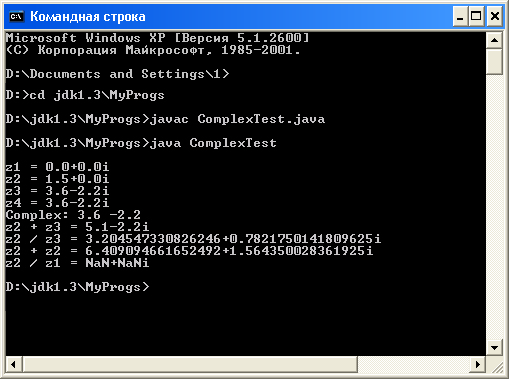
Рис. 2.3. Вывод программы  ComplexTest